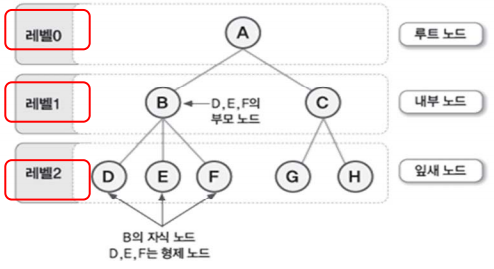
자료를 포함하고 있는 노드(node)와 노드들 간의 관계(edge)로 구성되며, 임의의 두 노드는 부모(parent)와 자식(child) 관계만을 갖는다.
root node: 최상단의 부모 노드를 갖지 않는 노드
leaf node: 트리에서 자식 노드를 가지고 있지 않는 노드
Internal node: 루트 노드와 잎새 노드 제외한 나머지 노드
sibling node(형제 노드): 같은 부모를 가진 자식 노드
*트리의 특징
① 트리는 계층적 자료를 표현하는데 적합한 자료 구조이다.
② 트리에서 자료의 저장은 노드에 한다.
③ 트리에서 부모가 없는 노드를 루트 노드라고 하고 자식이 없는 노드를 잎새 노드라고 한다.
④ 이진 탐색 트리는 한번의 경로 탐색으로 자료의 유무 및 원하는 자료를 검색할 수 있다.
*이진(Binary) 탐색 트리
트리의 각 노드에서 자식 노드를 최대 2개까지 가질 수 있는 트리이며 각 노드에서 자식은 왼쪽(left) 자식 노드와 오른쪽(right) 자식 노드로 구분한다.
트리 구성 시 입력되는 자식 노드에 있는 자료의 값이 부모 노드의 자료 값보다 작은 값을 가질 때 부모의 왼쪽 자식 노드에 위치하고, 부모 노드의 자료 값보다 큰 값을 가질 때 오른쪽 자식 노드에 위치시킨다.
이진탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제가 가능하다.
*이진(Binary) 탐색 트리의 예
1. L, H, C, R, J, M, N, A, E, I, Z 데이터에서 I 검색
루트 노드인 L을 시작으로 I를 찾을 때까지 검색 값 I와 각 노드의 값을 비교하여 I가 노드 값보다 작으면 왼쪽 경로로, 크면 오른쪽 경로로 노드 탐색
L → H → J → I

2. 아래의 작업들을 배열의 크기가 3인 큐에서 진행할 때에 작업이 불가능해지는 시점은 언제인가?
enQueue(/가/) → enQueue(/나/) → deQueue() → enQueue(/다/) → deQueue()
→ enQueue(/라/) → enQueue(/마/)

작업이 불가능해지는 시점은 존재하지 않는다.
'공부 > 자료 구조 및 알고리즘' 카테고리의 다른 글
| 자료의 탐색 - 이진 탐색(Binary search) (0) | 2019.07.13 |
|---|---|
| 자료의 탐색 - 순차 탐색(Sequential search) (0) | 2019.07.12 |
| 문재 해결을 위한 기본적 접근 방법 - 큐(Queue) (0) | 2019.07.06 |
| 문재 해결을 위한 기본적 접근 방법 - 스택(Stack) (0) | 2019.06.27 |
| 문재 해결을 위한 기본적 접근 방법 - 배열(Array) (0) | 2019.06.27 |



