* 해당 포스트는 PC환경에 최적화 되어있습니다.
* 쉽게 배우는 알고리즘 개정판 교재로 공부했으며 학교에서 배운 내용과 섞어서 정리한 포스트입니다.
* 저작권 문제는 hjl3066@gmail.com으로 연락주시면 빠르게 조치하겠습니다.
앞선 포스트에서 알고리즘 설계에 대해 알아보았다. 이번에는 알고리즘의 분석에 대해 알아보자.
알고리즘 분석의 필요성
어떤 알고리즘을 설계하고 나면 이 알고리즘이 소모하는 리소스와 소요 시간 등을 분석해야할 필요가 있다.
알고리즘 분석은 대부분 소요 시간에 중점을 둔다. 그렇다고 소요 시간 외의 자원들을 신경쓰지 않는 것은 아니다. 리소스와 같은 자원은 주어진 범위 내에서는 문제가 없지만 때로는(데이터 통신과 같은 경우) 소요 시간 보다 더 중요할 수 있다.
바람직한 알고리즘
• 명확해야 한다.
- 모호하지 않고 이해하기 쉽게
- 지나친 기호적 표현 지양
- 명확성을 해치지 않는 선에서 일반언어 사용 무방
• 효율적이어야 한다.
- 입력의 크기가 충분히 클 경우를 고려
- 충분히 큰 입력에 대하여, 같은 문제를 해결하는 알고리즘의 효율성에 따라 수행시간이 수백만 배 이상 차이날 수 있음.
알고리즘의 수행 시간
알고리즘의 수행 시간은 입력의 크기에 대해 시간이 어떤 비율로 소모되는지로 표현한다.
알고리즘의 수행 시간을 좌우하는 기준은 다양하게 잡을 수 있다.
for 루프의 반복 횟수, 특정한 행이 수행되는 횟수, 함수의 호출 횟수 등...
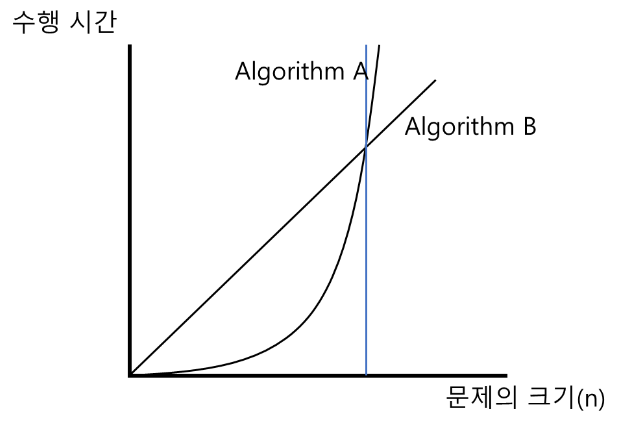
파란선 이전과 이후에 따라 알고리즘 A와 B의 효율이 달라진다.
다시 말해 문제의 크기가 클수록 알고리즘 B가 효율이 좋아지지만,
문제의 크기가 작을수록 알고리즘 A의 효율이 더 좋다.
아래의 그래프와 표를 통해 자주보게될 수행 시간과 문제의 크기에 따른 효율을 알 수 있다.

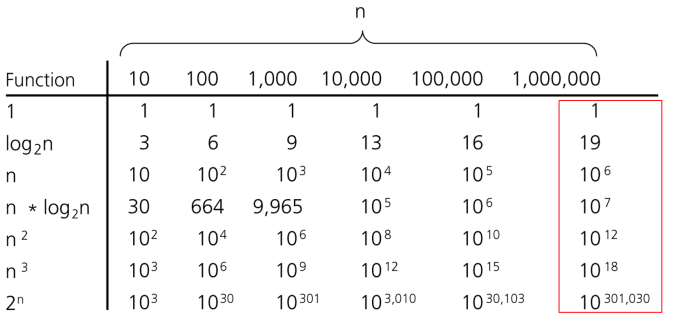
알고리즘의 수행 시간 예
sample1(A[], n) {
k = ⌊ n/2 ⌋; //⌊ ⌋ 내림 기호
return A[k];
}입력값 n을 2로 나누고 내리는 중간값 찾기 알고리즘이다.
배열 n에 상관없이 일정한 상수 시간이 소요된다.
sample2(A[], n) {
sum ← 0;
for i ← 1 to n;
sum ← sum + A[i];
return sum;
}0 ~ n까지의 모든 숫자를 더하는 알고리즘이다.
for 루프가 n번 반복되는 n에 비례하는 시간이 소요된다.
sample3(A[], n) {
sum ← 0;
for i ← 1 to n
for j ← 1 to n
sum ← sum + A[i] * A[j];
return sum;
}배열 A의 모든 원소를 곱한 합을 구하는 알고리즘이다.
for루프가 2중으로 중첩되어 있으므로 n x n번 반복된다.
각 루프에서 곱셈과 덧셈 한 번씩 상수시간이 소요된다.
n²에 비례하는 시간이 소요된다.
sample4(A[], n) {
sum ← 0;
for i ← 1 to n
for j ← 1 to n {
k ← A[1 ... n]에서 임의로 ⌊ n/2 ⌋개를 뽑을 때 이들 중 최대값;
sum ← sum + k;
}
return sum;
}뭐하는 알고리즘인지 몰라도 소요 시간은 알 수 있다.
n/2개 원소 중 최대값을 찾는 것을 for 루프로 2중 중첩되어 있으므로
n/2 * n² = n³/2, 큰 단위에서 /2는 거의 의미가 없기에 날리면
n³에 비례하는 시간이 소요된다.
sample5(A[], n) {
sum ← 0;
for i ← 1 to n - 1
for j ← i + 1 to n
sum ← sum + A[i] * A[j];
return sum;
}n개의 원소의 i보다 큰 모든 j원소의 쌍을 곱하는 알고리즘이다.
이제 딱봐도 감온다 n²에 비례하는 시간이 소요된다.
factorial(n) {
if (n == 1)
return 1;
return n * factorial(n - 1);
}자기호출 알고리즘이다. factorial의 총 호출 횟수는 n번이다.
n에 비례하는 시간이 소요된다.
재귀와 귀납적 사고
자기호출은 컴퓨터 과학 이론의 근간을 이루는 중요한 개념이다.
문제 해결 과정에서 자신과 똑같지만 크기만 다른 문제를 발견하고, 이들의 관계를 파악함으로써 문제 해결에 간단하고 명료하게 접근하는 방식이다. 고등학교 수학에서 배우는 수학적 귀납법을 기억하고 있다면 도움될 것이다.
재귀적 구조는 어떤 문제 안에 크기만 다를 뿐 성격이 똑같은 작은 문제들이 포함되어 있는 것이다.
피보나치 수열과 팩토리얼, 수열의 점화식(등차 수열)이 그 예이다.
뒤에 자세히 배우겠지만 자기호출 알고리즘의 좋은 예인 병합 정렬을 미리 살펴보자.
mergeSort(A[], p, r) {
if (p < r) then {
q ← ⌊ (p + r) / 2 ⌋;
mergeSort(A, p, q); //재귀
mergeSort(A, q + 1, r); //재귀
merge(A, p, q, r);
}
}
merge(A[], p, q, r) {
정렬되어 있는 두 배열 A[p ... q]와 A[q + 1 ... r]을 합쳐
정렬된 하나의 배열 A[p ... r]을 만든다.
}반으로 자르고 재귀시켜서 다시 반으로 자르고를 반복하여 병합하면 정렬이 되는 알고리즘이다.
알고리즘의 분석
크기가 작은 문제는 알고리즘의 효율성이 크게 차이나지 않아 효율성이 그리 중요하지 않다. 그러므로 비효율적인 알고리즘도 무방하다.
크기가 충분히 큰 문제는 알고리즘의 효율성이 중요하다. 비효율적인 알고리즘은 소요 시간에 치명적이다.
▶ 입력의 크기가 충분히 큰 경우에 대한 분석을 점근적 분석이라고 한다.
'공부 > 알고리즘' 카테고리의 다른 글
| 03. 점화식과 점근적 복잡도 분석 (0) | 2023.01.11 |
|---|---|
| 02. 알고리즘 설계와 분석 2 - 점근적 표기법 (0) | 2023.01.06 |
| 01. 알고리즘이란? (0) | 2023.01.05 |
| 06. 검색 트리 - 레드 블랙 트리(RB Tree) (0) | 2022.12.20 |
| 06. 검색 트리 - 이진 검색 트리 (0) | 2022.12.19 |


